TP - le problème des reines

Licence CC BY-NC-ND, Thierry Parmentelat

modalités¶

vous êtes censé travailler en local sur votre ordi; le zip contient

ce notebook
un dossier media/ avec les figures
un fichier de test test_rooks_and_queens.py

l’idée générale, c’est d’utiliser un workflow classique, qui consiste en ceci :

vous commencez à travailler directement dans le notebook
une fois que le code marche raisonnablement, vous extrayez votre code pour le ranger dans un module Python normal, qui s’appelle rooks_and_queens.py
que vous pouvez alors importer depuis le notebook, toutes les visualisations continuent à fonctionner
et en plus comme ça le code devient réutilisable - depuis un autre notebook, ou depuis un programme classique
et en plus on peut le tester facilement

en effet, le fichier fourni de test test_rooks_and_queens.py sait valider votre code; c’est un exercice pour commencer à utiliser un framework de test
ici on va utiliser pytest, si nécessaire installez cet outil avec pip install pytest (eh oui :)

et avec ce setup

depuis le notebook, vous pouvez importer rooks_and_queens et mettre au point votre code
et depuis le terminal, vous pouvez lancer les tests en faisant (dans le dossier en question bien sûr)

# vous pouvez faire `pytest` tout court aussi
$ pytest test_rooks_and_queens.py
================================ test session starts ================================
platform darwin -- Python 3.10.8, pytest-7.2.0, pluggy-1.0.0
rootdir: /Users/tparment/git/flotpython-exos/python-tps/queens
plugins: anyio-3.6.2
collected 3 items

test_rooks_and_queens.py ...                                                  [100%]

================================ 3 passed in 14.19s =================================

les tours¶

on se place sur un échiquier de taille $n \times n$
on cherche à écrire un générateur qui énumère les positions de $n$ tours qui ne se menacent pas les unes les autres

système de coordonnées¶

les positions que l’on cherche ont toutes une bonne propriété, c’est que de par l’énoncé du problème on ne peut avoir qu’une position occupée sur chaque colonne de l’échiquier

aussi, pour se simplifier la vie

plutôt que de manipuler des positions sur l’échiquier sous la forme de tuples $(x, y)$ ,
on va se contenter d’un tuple - ou d’une liste, peu importe - de coordonnées Y

c’est ainsi qu’on va représenter une position, comme par exemple celle-ci

par le tuple (0, 4, 1, 2, 3) qui donne les coordonnées en Y dans les colonnes successives (ici le dessin est fait avec matplotlib, du coup les Y sont descendants, mais l’orientation n’a pas vraiment d’importance)

ce qu’on doit pouvoir faire¶

# dans ce notebook on importe le code de démonstration
# mais bien sûr à la fin de l'exercice vous pourrez exécuter ça
# avec votre propre code
from rooks_and_queens import rooks

r3 = rooks(3)

# une première solution
next(r3)

[0, 1, 2]

# une autre
next(r3)

[1, 2, 0]

# et ainsi de suite
next(r3)

[2, 0, 1]

# on a déjà consommé 3 des 6 positions; du coup ...
# si maintenant on fait une boucle for on ne voit plus que les 3 dernières !

for position in r3:
    print(position)

[1, 0, 2]
[0, 2, 1]
[2, 1, 0]

à quoi ça ressemble ?¶

il ne vous aura pas échappé que le problème est équivalent à énumérer les permutations de $n$ (et c’est d’ailleurs pour ça qu’on choisit de retourner une liste d’entiers, et non pas des tuples)

donc du coup on pourrait faire tout simplement

from itertools import permutations

def cheated_rooks(n):
    return permutations(range(n))

# et en effet
for p in cheated_rooks(3):
    print(p)

(0, 1, 2)
(0, 2, 1)
(1, 0, 2)
(1, 2, 0)
(2, 0, 1)
(2, 1, 0)

mais bon pour cet exercice on va vous demander de réfléchir à une façon de faire ça vous-même à la main, sans recourir à itertools donc...

# à vous d'écrire le code de la fonction (un générateur donc) rooks
#def rooks():
#    ...

les reines¶

forts de cet outil, on va maintenant vous demander d’énumérer les positions des reines qui ne se menacent pas les unes les autres

# ce qui donnerait ceci

from rooks_and_queens import queens

for p in queens(5):
    print(p)

[2, 0, 3, 1, 4]
[0, 3, 1, 4, 2]
[3, 1, 4, 2, 0]
[1, 4, 2, 0, 3]
[4, 2, 0, 3, 1]
[1, 3, 0, 2, 4]
[3, 0, 2, 4, 1]
[0, 2, 4, 1, 3]
[2, 4, 1, 3, 0]
[4, 1, 3, 0, 2]

for p in queens(6):
    print(p)

[3, 0, 4, 1, 5, 2]
[4, 2, 0, 5, 3, 1]
[1, 3, 5, 0, 2, 4]
[2, 5, 1, 4, 0, 3]

# votre code pour définir queens
#def queens():
#    ...

calculer la taille (longueur) d’un générateur¶

on ne peut pas utiliser len() sur un générateur (pourquoi ?)
comment feriez-vous pour calculer le nombre d’éléments dans un générateur ?

# écrivez generator_size
# ATTENTION quand même à NE PAS créer une liste dans ce code
# car comme résultat on veut un entier hein
# pas besoin de consommer toute la mémoire de l'ordi pour ça hein !

from rooks_and_queens import generator_size
generator_size(queens(8))

92

dessin¶

si vous avez fini avant tout le monde, dessinez les résultats avec numpy.imshow, (ou autre outil de visualisation de votre choix)

%matplotlib inline

from rooks_and_queens import draw_position

for p in queens(4):
    print(p)
    draw_position(p)

[2, 0, 3, 1]

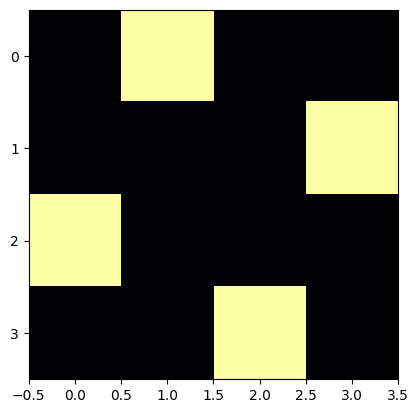
[1, 3, 0, 2]

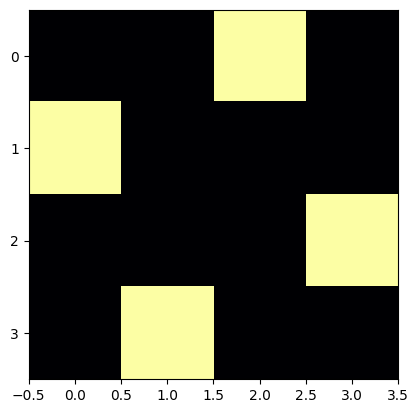
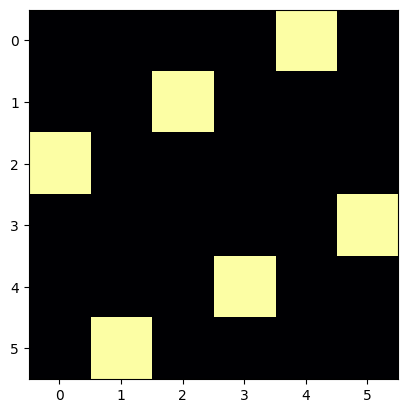
for p in queens(6):
    draw_position(p)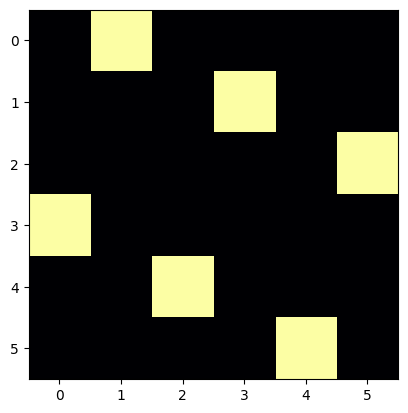

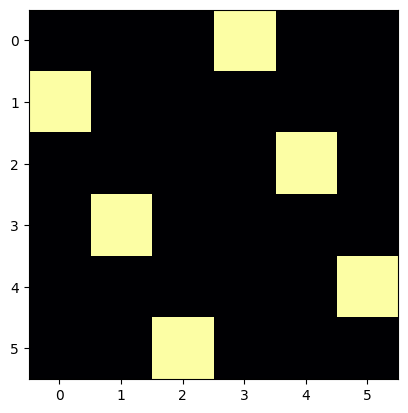
fin de la partie obligatoire¶

jusqu’ici c’est plutôt facile - ou court en tous cas; pour info ma correction tient en

7 lignes pour rooks
7 lignes pour queens
2 lignes pour generator_size
draw_position est - de manière contrintuitive - bien plus long il faut dire que je suis passé par deux fonctions pour traduire entre les tuples d’entiers et le tableau numpy; en fait une seule aurait suffi, mais pour la suite j’ai tiré profit des deux

la partie qui suit est intéressante aussi, et pas tellement plus longue en fait (13 lignes pour uniques dans mon cas), n’hésitez pas à vous y essayer aussi.

éliminez les symétries¶

(un tout petit peu) plus dur, éliminez les symétries et rotations

il y a plein de façons d’envisager la question, idéalement on doit pouvoir écrire un itérateur uniques qu’on pourra en quelque sorte chainer avec les deux algorithmes qu’on vient d’écrire

# c'est à dire qu'on veut pouvoir écrire quelque chose comme ceci
from rooks_and_queens import uniques

# en fait les 4 solutions de queens(6) sont toutes les mêmes
# aussi quand on passe par uniques() il n'en reste qu'une

for p in uniques(queens(6)):
    draw_position(p)

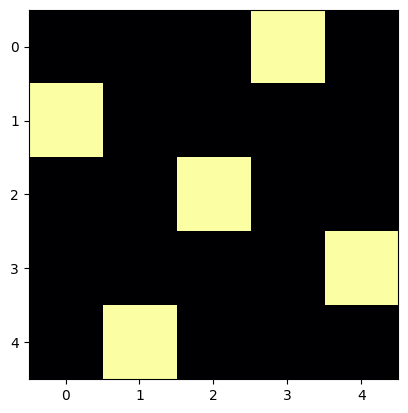
# en dimension 5 curieusement il y en a plus que pour n=6

for p in uniques(queens(5)):
    draw_position(p)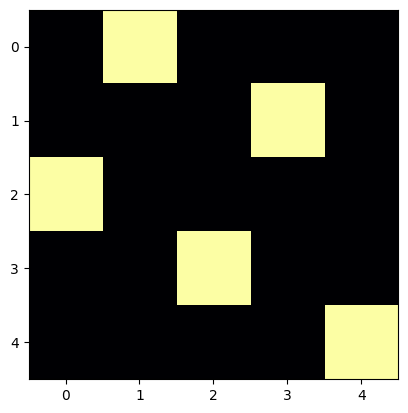

# combien reste-t-il de permutations uniques 
# une fois qu'on a éliminé les rotations et symétries
# sur les 120 de S5

generator_size(uniques(rooks(5)))

23

# et dans le cas de l'échiquier "normal"
# voici à peu près la performance que vous pouvez obtenir
# sans trop chercher à optimiser...

%timeit generator_size(uniques(rooks(8)))

421 ms ± 54 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)