TP - algos de base sur les graphes

Licence CC BY-NC-ND, Thierry Parmentelat

introduction¶

dans ce TP nous allons

• étudier quelques algorithmes de base des graphes

• et les implémenter

et pour cela nous aurons besoin

• de choisir une structure de données

• d’être capables de lire un graphe depuis un fichier texte

comme nous n’avons pas encore étudié les classes, nous allons nous restreindre à utiliser uniquement les types de base de Python - listes, tuples, dictionnaires et ensembles

formalisation¶

nous nous intéressons aux graphes valués, qu’on peut définir formellement comme un triplet $G =(V, E, W)$, où

• $V$ est un ensemble quelconque, qu’on appelle l’ensemble des sommets (vertices) du graphe,

• $E$ est une partie de $V\times V$; les couples $(v_1, v_2)$ dans $E$ s’appellent les arêtes (edges) du graphe

• $W$ est une fonction $E\rightarrow\mathbb{N}$, qui attache à chaque arête une valeur, un poids (weight),
  qui peut être interprété aussi selon les usages comme une distance entre les sommets concernés; ou tout autre chose d’ailleurs, par exemple une durée…

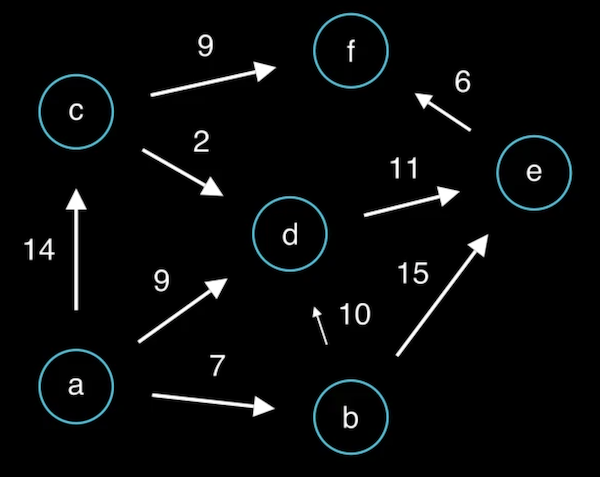
familles de problèmes¶

dans la littérature, les problèmes de plus court chemin participent de plusieurs niveaux de complication, selon qu’on cherche la distance la plus courte

• entre deux sommets spécifiques (single pair problem), e.g. de a à f

• depuis un sommet spécifique vers tous les autres sommets (single source problem)

• entre tous les sommets (all pairs problem)

• depuis tous les sommets vers un sommet spécifique (single sink problem)

en toute généralité on peut aussi considérer le cas où les poids peuvent être négatifs

pour notre part et dans la suite, on se placera dans le cas usuel où toutes les distances sont strictement positives, et on va se concentrer sur le single pair problem, c’est-à-dire avec une source et une destination spécifiques.

structure de données¶

pour ce TP, on va se limiter à des sommets qui soient des chaines de caractères

quelles options voyez-vous pour modéliser un graphe par un objet Python ?

liste de listes¶

# par exemple
graph_as_list = [
  ['a', 14, 'c'],
  ['a', 9, 'd'],
  ['a', 7, 'b'],
  ['a', 7, 'b'],
  ['b', 10, 'd'],
  ...
]

matrice¶

si on veut coder le graphe comme une matrice, on a besoin aussi de garder les noms des sommets

# par exemple
import numpy as np
graph_as_matrix = (
    np.array([
        [0, 7,14, 9, 0, 0],
        [0, 0, 0,10,15, 0],
        [0, 0, 0, 2, 0, 9],
        [0, 0, 0, 0,11, 0],
        [0, 0, 0, 0, 0, 6],
        [0, 0, 0, 0, 0, 0]]),
    ['a', 'b', 'c', 'd', 'e', 'f'])

autres idées ?¶

# comment feriez-vous ?
my_graph = ...

lecture d’un fichier¶

la plupart du temps on va aller chercher ces données sur Internet auprès de dépôts de type Open-Data, et sur Internet on ne trouve pas des objets Python (matrice ou liste ou dictionnaire ou ...), on trouve seulement du texte (même quand c’est du HTML ou du XML ou du JSON ou du CSV, c’est toujours du texte, plus ou moins facile à transformer en objets Python)

donc pour pouvoir stocker / échanger les données de type graphe, on a besoin aussi d’un format textuel
c’est quoi un format textuel ? simplement un ensemble de conventions qui décrivent comment on peut écrire un graphe sous forme de texte

dans notre cas, nous allons choisir la forme la plus simple possible :

• une ligne par arête

• sous la forme source, destination, poids

ce qui donnerait (par exemple) pour notre graphe témoin le fichier (ouvrez-le sous vs-code) data/graph.csv

a,b,7
a,d,9
a,c,14
b,d,10
b,e,15
c,d,2
c,f,9
d,e,11
e,f,6

exo #1: parse_graph¶

notre premier exercice va donc consister à écrire une fonction qui

• prend en paramètre un nom de fichier - comme data/graph.csv

• ouvre le fichier en question et le lit

• pour construire la structure de données qu’on a choisie

• qu’elle retourne à l’appelant (c’est-à-dire avec return, quoi)

mais en fait, on a choisi quoi comme structure de données ?
pour éviter les inconvénients des listes et des matrices, on va représenter un graphe comme

• un dictionnaire

• où chaque clé est un sommet de départ (une chaine donc)

• et où chaque valeur est à son tour un dictionnaire

  • où chaque clé est un sommet (d’arrivée)

  • et où chaque valeur est un poids

# ce qui donnerait pour notre graphe témoin

G = {
    'a': {'b': 7, 'd': 9, 'c': 14},
    'b': {'d': 10, 'e': 15},
    'c': {'d': 2, 'f': 9},
    'd': {'e': 11},
    'e': {'f': 6},
    'f' : {},
}

# rappel: pour découper une chaine

'a,b,12'.split(',')

# rappel: pour convertir une chaine en entier

int('12 ')

# rappel: pour nettoyer une chaine

' a,b,12\n'.strip()

# ou si on préfère

' a,b,12\n'.rstrip()

à vous de jouer¶

# à vous d'écrire cette fonction

def parse_graph(filename):
    ...

pour vérifier, inspectez visuellement votre résultat
vérifiez aussi/surtout que les poids sont bien des entiers et pas des chaines

# ceci doit vous afficher un dictionnaire de dictionnaires

parse_graph("data/graph.csv")

# et ceci doit être True

parse_graph("data/graph.csv") == G

# et ceci doit être True aussi

import json

with open("data/graph-2.json") as f:
    g2ref = json.load(f) 
g2ref == parse_graph("data/graph-2.csv")

# et ceci doit être True aussi

with open("data/graph-3.json") as f:
    g3ref = json.load(f) 
g3ref == parse_graph("data/graph-3.csv")

nombre de sommets¶

exo #2: number_vertices¶

écrivez une fonction qui retourne le nombre de sommets du graphe

def number_vertices(graph):
    """
    returns number of vertices
    
    Parameters:
      graph: implemented as a dictionary of adjacency dictionaries
      
    Returns:
      int: number of vertices
    """
    ...

pour vérifier¶

# pour vérifier: doit retourner True

(   number_vertices(G) == 6
and number_vertices(g2ref) == 6
and number_vertices(g3ref) == 7)

atteignabilité¶

maintenant que nous avons une structure de données, nous allons pouvoir en faire quelque chose d’utile
le premier algorithme que nous allons voir consiste à calculer l’ensemble des sommets que l’on peut atteindre en partant d’un sommet donné

commençons par voir un exemple

# un graphe voisin de notre graphe témoin, mais avec des boucles
# parce que sinon c'est pas drôle

reach = parse_graph("data/reach.csv")

# pour le visualiser:
# installer graphviz avec 
# conda install graphviz
# (sinon ce n'est pas du tout critique)

try:
    from IPython.display import display
    from data.graphs import to_graphviz
    with open("data/reach.json") as f:
        reach = json.load(f)
    display(to_graphviz(reach, "neato"))
except Exception as exc:
    print("graphical output not available, but no worries....")
    # print(f"{type(exc)}: {exc}")

There is no layout engine support for "neato"
 Use one of: dot

---------------------------------------------------------------------------
CalledProcessError                        Traceback (most recent call last)
File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/backend/execute.py:88, in run_check(cmd, input_lines, encoding, quiet, **kwargs)
     87 try:
---> 88     proc.check_returncode()
     89 except subprocess.CalledProcessError as e:

File /usr/lib/python3.14/subprocess.py:509, in CompletedProcess.check_returncode(self)
    508 if self.returncode:
--> 509     raise CalledProcessError(self.returncode, self.args, self.stdout,
    510                              self.stderr)

CalledProcessError: Command '[PosixPath('dot'), '-Kneato', '-Tsvg']' returned non-zero exit status 1.

During handling of the above exception, another exception occurred:

CalledProcessError                        Traceback (most recent call last)
File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/jupyter_integration.py:98, in JupyterIntegration._repr_mimebundle_(self, include, exclude, **_)
     96 include = set(include) if include is not None else {self._jupyter_mimetype}
     97 include -= set(exclude or [])
---> 98 return {mimetype: getattr(self, method_name)()
     99         for mimetype, method_name in MIME_TYPES.items()
    100         if mimetype in include}

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/jupyter_integration.py:112, in JupyterIntegration._repr_image_svg_xml(self)
    110 def _repr_image_svg_xml(self) -> str:
    111     """Return the rendered graph as SVG string."""
--> 112     return self.pipe(format='svg', encoding=SVG_ENCODING)

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/piping.py:104, in Pipe.pipe(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
     55 def pipe(self,
     56          format: typing.Optional[str] = None,
     57          renderer: typing.Optional[str] = None,
   (...)     61          engine: typing.Optional[str] = None,
     62          encoding: typing.Optional[str] = None) -> typing.Union[bytes, str]:
     63     """Return the source piped through the Graphviz layout command.
     64 
     65     Args:
   (...)    102         '<?xml version='
    103     """
--> 104     return self._pipe_legacy(format,
    105                              renderer=renderer,
    106                              formatter=formatter,
    107                              neato_no_op=neato_no_op,
    108                              quiet=quiet,
    109                              engine=engine,
    110                              encoding=encoding)

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/_tools.py:185, in deprecate_positional_args.<locals>.decorator.<locals>.wrapper(*args, **kwargs)
    177     wanted = ', '.join(f'{name}={value!r}'
    178                        for name, value in deprecated.items())
    179     warnings.warn(f'The signature of {func_name} will be reduced'
    180                   f' to {supported_number} positional arg{s_}{qualification}'
    181                   f' {list(supported)}: pass {wanted} as keyword arg{s_}',
    182                   stacklevel=stacklevel,
    183                   category=category)
--> 185 return func(*args, **kwargs)

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/piping.py:121, in Pipe._pipe_legacy(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
    112 @_tools.deprecate_positional_args(supported_number=1, ignore_arg='self')
    113 def _pipe_legacy(self,
    114                  format: typing.Optional[str] = None,
   (...)    119                  engine: typing.Optional[str] = None,
    120                  encoding: typing.Optional[str] = None) -> typing.Union[bytes, str]:
--> 121     return self._pipe_future(format,
    122                              renderer=renderer,
    123                              formatter=formatter,
    124                              neato_no_op=neato_no_op,
    125                              quiet=quiet,
    126                              engine=engine,
    127                              encoding=encoding)

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/piping.py:149, in Pipe._pipe_future(self, format, renderer, formatter, neato_no_op, quiet, engine, encoding)
    146 if encoding is not None:
    147     if codecs.lookup(encoding) is codecs.lookup(self.encoding):
    148         # common case: both stdin and stdout need the same encoding
--> 149         return self._pipe_lines_string(*args, encoding=encoding, **kwargs)
    150     try:
    151         raw = self._pipe_lines(*args, input_encoding=self.encoding, **kwargs)

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/backend/piping.py:212, in pipe_lines_string(engine, format, input_lines, encoding, renderer, formatter, neato_no_op, quiet)
    206 cmd = dot_command.command(engine, format,
    207                           renderer=renderer,
    208                           formatter=formatter,
    209                           neato_no_op=neato_no_op)
    210 kwargs = {'input_lines': input_lines, 'encoding': encoding}
--> 212 proc = execute.run_check(cmd, capture_output=True, quiet=quiet, **kwargs)
    213 return proc.stdout

File /__w/exos-python/exos-python/venv/lib/python3.14/site-packages/graphviz/backend/execute.py:90, in run_check(cmd, input_lines, encoding, quiet, **kwargs)
     88     proc.check_returncode()
     89 except subprocess.CalledProcessError as e:
---> 90     raise CalledProcessError(*e.args)
     92 return proc

CalledProcessError: Command '[PosixPath('dot'), '-Kneato', '-Tsvg']' returned non-zero exit status 1. [stderr: 'There is no layout engine support for "neato"\n Use one of: dot\n']

# voilà ce qu'on doit trouver sur ce graphe comme sommets atteignables:

import pickle

with open("data/reach.pickle", 'rb') as f:
    reach_reachables = pickle.load(f)

reach_reachables

for vertex, expected_reachables in reach_reachables.items():
    print(f"en partant de {vertex} → {expected_reachables}")

en partant de a → {'e', 'c', 'f', 'a', 'd', 'b'}
en partant de b → {'e', 'c', 'f', 'a', 'd', 'b'}
en partant de d → {'e', 'c', 'f', 'a', 'd', 'b'}
en partant de c → {'e', 'c', 'f', 'a', 'd', 'b'}
en partant de e → {'f', 'e'}
en partant de f → {'f', 'e'}

la difficulté¶

l’anti-loop¶

si on parlait d’arbres et non pas de graphes, on pourrait s’en sortir très simplement avec un parcours récursif en profondeur

mais ici on a des graphes, avec possiblement des cycles, et donc il faut faire un peu attention, notamment à ne pas boucler à l’infini

quelles méthodes est-ce que vous voyez pour éviter justement de boucler (pour éviter de repasser plusieurs fois au même endroit ?)

indice soyez attentifs à la performance; on veut pouvoir utiliser cet algorithme avec des graphes très gros…

quand est-ce qu’on s’arrête ?¶

comment fait-on pour décider de s’arrêter ?

ne pas modifier le sujet de la boucle¶

sans transition, mais c’est sans doute le bon moment pour signaler une limitation de Python, qui est qu’on ne peut pas modifier un objet sur lequel on est en train de faire une boucle

illustration :

# on ne peut pas modifier un objet sur lequel on boucle
# ici un dictionnaire pour commencer

D = {'a': 'b', 'c': 'd'}

try:
    for k, v in D.items():
        D[k+v] = v+k
except Exception as exc:
    print(f"OOPS {type(exc)} {exc}")

OOPS <class 'RuntimeError'> dictionary changed size during iteration

S = {'a', 'b'}

# c'est vrai pour tous les containers - ici un ensemble
# et c'est vrai que ce soit pour ajouter ou pour enlever

try:
    for s in S:
        S.remove(s)
except Exception as exc:
    print(f"OOPS {type(exc)} {exc}")

OOPS <class 'RuntimeError'> Set changed size during iteration

exo #3: reachables¶

je ne vous donne pas davantage d’indices, je vous laisse écrire ceci

# votre code 

def reachables(graph, s):
    """
    computes the set of reachable vertices in a graph from source s

    Parameters:
      graph: a graph implemented as a dict of adjacency dicts
      s: the source vertex
    Returns:
      a set of vertices in graph
    """
    ...

pour vérifier¶

vous pouvez vérifier visuellement en comparant vos résultats avec ceux qu’on a vus dans l’exemple

# pour le debug

for s in reach:
    print(f"depuis {s} → {reachables(reach, s)}")

depuis a → None
depuis b → None
depuis d → None
depuis c → None
depuis e → None
depuis f → None

# pareil mais orienté test et pas debug
# on teste le résultat sur chaque sommet

for vertex, expected_reachables in reach_reachables.items():
    print(f"en partant de {vertex} → {expected_reachables == reachables(reach, vertex)}")

en partant de a → False
en partant de b → False
en partant de d → False
en partant de c → False
en partant de e → False
en partant de f → False

# pareil sur le graphe témoin du départ
# on énumère à la main les sommets à tester 
# et les résultats attendus

G_expected_reachables = [
    ('a', {'a', 'b', 'c', 'd', 'e', 'f'}),
    ('b', {'b', 'd', 'e', 'f'}),
    ('c', {'c', 'd', 'e', 'f'}),
    ('d', {'d', 'e', 'f'}),
    ('e', {'e', 'f'}),
    ('f', {'f'}),
]

# on vérifie pour chacun qu'on
# obtient bien le résultat attendu
for (vertex, expected_reachables) in G_expected_reachables:
    computed = reachables(G, vertex)
    if computed != expected_reachables:
        print(f"ERROR since {vertex}: found {computed} != {expected_reachables}")
    else:
        print(f"OK since {vertex} → {computed}")

ERROR since a: found None != {'c', 'f', 'a', 'b', 'd', 'e'}
ERROR since b: found None != {'d', 'f', 'b', 'e'}
ERROR since c: found None != {'c', 'f', 'e', 'd'}
ERROR since d: found None != {'d', 'f', 'e'}
ERROR since e: found None != {'f', 'e'}
ERROR since f: found None != {'f'}

plus courte distance¶

on va pouvoir aussi calculer le plus court chemin entre deux noeuds d’un graphe
pour cela nous allons utiliser un algorithme très classique, connu sous le nom d’algorithme de Dijkstra

c’est un algorithme très utilisé; lorsque vous demandez à une app de vous calculer un itinéraire par exemple, c’est bien sûr comme ça que c’est calculé, et il y a de fortes chances pour que l’algorithme utilisé soit basé sur Dijkstra; remarquez que ce qu’on a appelé distance jusqu’ici, ça peut être aussi une durée, ou n’importe quoi d’autre bien entendu.

l’idée générale est assez simple :

• on énumère tous les chemins partant du sommet de départ

• dans l’ordre croissant de longueur

et du coup si/quand on arrive au sommet d’arrivée, on a forcément trouvé le plus court chemin entre les deux

illustration¶

voici une illustration de cet algorithme, sur notre graphe témoin, entre les noeuds a et f

l’algorithme¶

en français :

• on se dote d’un moyen de ‘marquer’ les noeuds :

  • on a deux types de noeud : visité ou non visité

  • les noeuds visités sont marqués avec un entier qui dénote la longueur d’un chemin (du plus court chemin en fait) depuis a

• au départ, seul le noeud $a$ est marqué avec une distance nulle

• on fait une boucle, et à chaque tour :

  • on localise toutes les arêtes qui lient un noeud visité à un noeud non visité

  • pour chacune de ces arêtes $s ― (w) → d$, on calcule la somme
    $marque(s) + w$

  • on sélectionne l’arête $s_0 ― (w_0) → d_0$ pour laquelle cette somme est la plus petite

  • on marque $d_0$ comme visité avec $marque(s_0) + w_0$

• on arrête la boucle lorsque, soit

  • on atteint la destination (ici $d_0 == f$)
    on a trouvé la distance la plus courte, qui est la marque de $f$

  • ou bien s’il n’y a plus d’arête qui satisfasse le critère
    ça signifie que $f$ n’est pas atteignable depuis $a$

question¶

• quels moyens (structures de données) voyez-vous pour matérialiser avec des objets Python la notion de marque ?

terminaison d’un algo avec les notebooks

ceci est une digression, mais c’est facile d’écrire par accident un algo qui boucle (i.e. qui ne termine jamais)

• lorsque ça arrive dans un notebook, l’affichage ressemble à In [*] comme ci-contre

• il faut alors interrompre le kernel

• on peut le faire par le menu Kernel → Interrupt

• ou encore en tapant 2 fois la touche i en mode Commande

Rappel :

• la cellule courante a un bandeau bleu en mode Commande, et un bandeau vert en mode Édition

• le mode Édition c’est pour insérer du texte, donc si vous tapez i i en mode édition, ça insère ii dans votre notebook, évidemment

pour les forts¶

à ce stade si vous êtes relativement confortable avec Python, vous devez pouvoir écrire une fonction qui calcule la distance la plus courte entre deux noeuds du graphe
n’hésitez pas alors à passer directement à la section “exo #4”, quitte à remonter voir les indices ensuite

des indices pour les autres¶

je décortique un peu pour ceux qui sont moins à l’aise

comment itérer sur le graphe¶

quelques rappels/astuces qui peuvent servir dans ce contexte :

# on rappelle comment itérer sur un dictionnaire
# d'abord pour lister toutes les arêtes sortant d'un sommet
# il faut itérer sur le dictionnaire d'adjacences

s = 'b'           # s pour source
adj = G[s]        # adj pour adjacency

# voici comment on itère sur les arêtes sortant du vertex
# d pour destination, et w pour weight

for d, w in adj.items():
    print(s, '→', w, '→', d)

b → 10 → d
b → 15 → e

# du coup pour itérer sur toutes les arêtes

for s, adj in G.items():
    for d, w in adj.items():
        print(f"{s=} → {d=}")

s='a' → d='b'
s='a' → d='d'
s='a' → d='c'
s='b' → d='d'
s='b' → d='e'
s='c' → d='d'
s='c' → d='f'
s='d' → d='e'
s='e' → d='f'

# math.inf matérialise l'infini
import math

10**6 < math.inf

structure générale de l’algorithme¶

pour commencer la structure générale de la fonction ressemble à ceci

à ne pas prendre au pied de de la lettre, vous pouvez/devez changer/renommer/faire autrement comme vous le sentez...

def shortest_distance(graph, v1, v2):

    # initialisation
    # on se définit une variable locale à la fonction
    # qui matérialise le marquage

    visited = ...

    # ensuite on fait une boucle jusqu'à ce qu'une certaine condition soit remplie
    # souvenez-vous qu'on peut sortir d'un while avec 'break' - ou aussi 'return' d'ailleurs
    while True:

        # on va calculer les arêtes qui font partie de la bordure
        edges = set()

        # on énumère toutes les arêtes, et on ajoute dans
        # edges celles qui satisfont le critère
        # for ...
        #    for ...
        #      if ...
        #         edges.add(...)
        #  

        # si on n'a aucune arête c'est que c'est raté
        if not edges:
            return

        # sinon on trouve la meilleure
        shortest_length = math.inf
        shortest_vertex = None
        for edge in edges:
            ... # trouver la plus courte
                # et mémoriser le sommet correspondant

        # marquer le sommet correspondant

        # regarder si c'est le sommet 
        if shortest_vertex == v2:
            return ...

exo #4: shortest_distance¶

# à vous d'écrire une fonction
# comme ceci

def shortest_distance(graph, v1, v2):
    """
    this function computes the length of the shortest path
    in graph between v1 and v2
    
    Parameters:
      graph: a graph described as a dictionary of dictionaries
      v1: the source vertex
      v2: the destination vertex
    Returns:
      int: the length of the shortest path, or None 
    """
    ...

vérifications¶

pour vérifier si votre code fonctionne :

# vérifiez que G est bien toujours notre graphe de référence
G

# doit renvoyer True

shortest_distance(G, 'a', 'f') == 23

shortest_distance(G, 'a', 'e') == 20

shortest_distance(G, 'c', 'b') is None

vérification avec un autre graphe en entrée¶

G2 = parse_graph('data/graph-2.csv')

G2

to_graphviz(G2, "dot")

oops: 'NoneType' object has no attribute 'items'

shortest_distance(G2, 'v1', 'v6')

avec quelques graphes denses¶

c’est l’occasion de parler un peu de l’instruction assert:

• sa fonction est de ne rien faire si l’expression associée est True

• par contre si elle est fausse, une exception AssertionError est levée

GD2 = parse_graph("data/dense-2.csv")
assert shortest_distance(GD2, "1x1", "2x2") == 4

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[38], line 2
      1 GD2 = parse_graph("data/dense-2.csv")
----> 2 assert shortest_distance(GD2, "1x1", "2x2") == 4

AssertionError: 

GD3 = parse_graph("data/dense-3.csv")
assert shortest_distance(GD3, "1x1", "3x3") == 6

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[39], line 2
      1 GD3 = parse_graph("data/dense-3.csv")
----> 2 assert shortest_distance(GD3, "1x1", "3x3") == 6

AssertionError: 

GD4 = parse_graph("data/dense-4.csv")
assert shortest_distance(GD4, "1x1", "4x4") == 8

---------------------------------------------------------------------------
AssertionError                            Traceback (most recent call last)
Cell In[40], line 2
      1 GD4 = parse_graph("data/dense-4.csv")
----> 2 assert shortest_distance(GD4, "1x1", "4x4") == 8

AssertionError: 

exo #5 : shortest_path¶

comment pourriez-vous adapter cet algorithme pour retourner aussi le chemin par lequel il faut passer ?

def shortest_path(graph, v1, v2):
    """
    same as shortest_distance but returns a tuple
    (distance, path)
    path being a list of vertices
    """
    # of course to write this function you will start
    # from your code for shortest_distance
    ...

pour vérifier¶

# je vous laisse le soin d'écrire le code pour tester

un graphe un peu plus réaliste¶

dans cette section on va se contenter d’utiliser ce qui précède, mais sur un graphe un peu plus gros
on est allé chercher les données dans ce dépôt sur github
il s’agit des relations entre les personnages d’un roman qui se situe dans le monde de Game of Thrones
on a choisi ces données car le graphe est de taille moyenne (71 sommets) mais reste suffisamment petit pour qu’on puisse vaguement le dessiner
remarquez que les données sont issues d’un dépôt 100% Java; le format de données ne dépend pas du tout du langage qu’on utilise pour les traiter, bien entendu

thrones_url = "https://raw.githubusercontent.com/pupimvictor/NetworkOfThrones/master/stormofswords.csv"

on va profiter de l’occasion pour voir comment aller chercher des données sur Internet

aller chercher et transformer la donnée¶

# si nécessaire, installer requests avec 
# $ pip install requests 

import requests

# voici l'idiome qui permet d'aller chercher 
# une page web à partir de son URL

get_request = requests.get(thrones_url)
text_data = get_request.text

# voilà à quoi ressemble le (début du) texte
# vous pouvez vérifier en pointant une nouvelle fenêtre 
# de votre navigateur vers l'url en question
text_data[:200]

maintenant le texte de la page Web est dans une variable Python (de type str donc)
il se trouve toutefois que

• nous avons écrit un code parse_graph qui traduit le contenu d’un fichier en un graphe, mais on n’a pas le code qui traduirait une chaine en un graphe

• en plus, la page web contient une première ligne en trop pour nous, il s’agit du nom des colonnes (vous vous rappelez peut-être le cours sur pandas, c’est fréquent pour un fichier .csv de contenir des métadata de ce genre dans les premières lignes)

donc bref, pour ne pas nous compliquer la vie, on va créer un fichier local avec le contenu du texte, moins la première ligne

une autre approche aurait pu être de re-factorer le code de parse_graph, pour permettre le parsing à partir d’une chaine, mais bon on ne va pas se compliquer la vie ici…; en plus ça nous donne une occasion d’utiliser ce qu’on a appris sur la création des fichiers

# écrivez le code qui sauve le contenu
# de la page web, sans la première ligne, 
# dans le fichier data/thrones.csv
# (le répertoire data/ existe déjà)

pour vérifier le contenu, regardez les 5 premières lignes qui devraient être

Aemon,Grenn,5
Aemon,Samwell,31
Aerys,Jaime,18
Aerys,Robert,6
Aerys,Tyrion,5
...

charger le graphe thrones¶

# une fois que le fichier local est OK, on peut utiliser notre
# code pour faire des calculs dans ce graphe

thrones = parse_graph("data/thrones.csv")

# should be True

number_vertices(thrones) == 107

on peut maintenant voir un peu à quoi il ressemble; enfin, si on a graphviz installé, et sinon, eh bien ce n’est pas grave !

try:
    visual_thrones = to_graphviz(thrones)
    visual_thrones.attr(size='28')
    display(visual_thrones)
except Exception as exc:
    print("too bad:", exc)

oops: 'NoneType' object has no attribute 'items'
too bad: 'NoneType' object has no attribute 'attr'

et maintenant on peut faire des calculs dans ce graphe

atteignabilité¶

# ce personnage semble assez central

len(reachables(thrones, 'Eddard')) == 88

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[50], line 3
      1 # ce personnage semble assez central
      2 
----> 3 len(reachables(thrones, 'Eddard')) == 88

TypeError: object of type 'NoneType' has no len()

# pas mal non plus

len(reachables(thrones, 'Bran')) == 42

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[51], line 3
      1 # pas mal non plus
      2 
----> 3 len(reachables(thrones, 'Bran')) == 42

TypeError: object of type 'NoneType' has no len()

# plus secondaire déjà

len(reachables(thrones, 'Davos')) == 3

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[52], line 3
      1 # plus secondaire déjà
      2 
----> 3 len(reachables(thrones, 'Davos')) == 3

TypeError: object of type 'NoneType' has no len()

# pas trop populaire non plus

len(reachables(thrones, 'Shireen')) == 4

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[53], line 3
      1 # pas trop populaire non plus
      2 
----> 3 len(reachables(thrones, 'Shireen')) == 4

TypeError: object of type 'NoneType' has no len()

plus court chemin¶

# des plus courts chemins
d, path = shortest_path(thrones, 'Eddard', 'Doran')
d == 15 and len(path) == 4 and 'Catelyn' in path

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[54], line 2
      1 # des plus courts chemins
----> 2 d, path = shortest_path(thrones, 'Eddard', 'Doran')
      3 d == 15 and len(path) == 4 and 'Catelyn' in path

TypeError: cannot unpack non-iterable NoneType object

d, path = shortest_path(thrones, 'Eddard', 'Margaery')
d == 17 and set(path) == {'Eddard', 'Sansa', 'Renly', 'Margaery'}

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[55], line 1
----> 1 d, path = shortest_path(thrones, 'Eddard', 'Margaery')
      2 d == 17 and set(path) == {'Eddard', 'Sansa', 'Renly', 'Margaery'}

TypeError: cannot unpack non-iterable NoneType object

(d, path) = shortest_path(thrones, 'Daenerys', 'Karl')
d == 38 and path == ['Daenerys', 'Viserys', 'Tyrion', 'Janos', 'Mance', 'Craster', 'Karl']

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Cell In[56], line 1
----> 1 (d, path) = shortest_path(thrones, 'Daenerys', 'Karl')
      2 d == 38 and path == ['Daenerys', 'Viserys', 'Tyrion', 'Janos', 'Mance', 'Craster', 'Karl']

TypeError: cannot unpack non-iterable NoneType object

shortest_path(thrones, 'Margaery', 'Eddard') is None

optimisation (optionnel / avancé)¶

quelque chose de louche¶

l’algorithme de plus court chemin que nous avons écrit jusqu’ici a surtout des avantages pédagogiques
l’intérêt est d’écrire un code qui s’écrit et se lit facilement

par contre, le lecteur affuté aura remarqué la chose suivante :

• à chaque itération de la boucle, on recalcule de zéro la frontière entre les sommets explorés et les autres

• or, d’un tour de boucle à l’autre, cette frontière change très peu, et uniquement autour du noeud que l’on vient d’explorer

ce qui peut nous laisser penser que, dans le cas de graphes plus substanciels que nos exemples jusqu’ici, l’algorithme risque d’avoir des performances sous-optimales (c’est une litote)

un graphe plus gros¶

pour n=4:

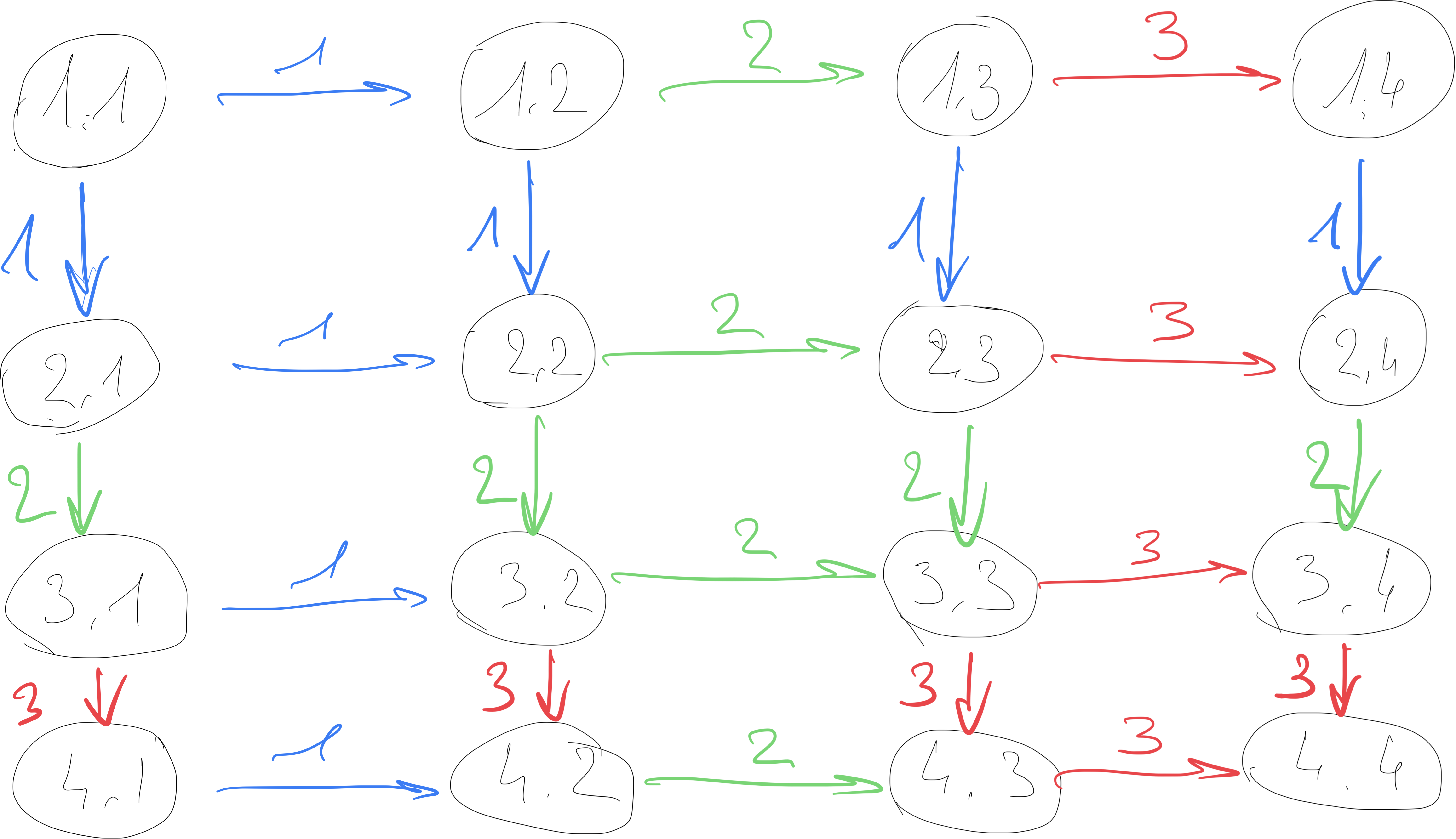
exercice: pour un entier $n$, écrire une fonction planar(n)
qui construit un graphe:

• qui contient $n^2$ sommets
  chacun étiqueté par un couple $(i, j), i\in[1..n], j\in[1..n]$

• où chaque sommet est connecté à ses voisins immédiats

  • $(i, j) \xrightarrow{i} (i+1, j)$ si $i<n$

  • $(i, j) \xrightarrow{j} (i, j+1)$ si $j<n$

from data.graphs import planar1 as planar
planar(4)

%timeit¶

on va utiliser la magic timeit:

• une magic est une instruction pour IPython (pas reconnu par Python standard)

• qui commence par un ou deux %

  • un seul %: s’applique à cette ligne

  • deux %%: s’applique à la cellule

en l’occurrence, timeit nous permet de mesurer le temps que prend une instruction
celle-ci est exécutée plusieurs fois, on prend ensuite la moyenne

pour faire la même chose en Python pur, voyez .. le module timeit

mesurons: n=10 et plus¶

# ça passe pas trop mal
# mais 3ms c'est quand même beaucoup pour 100 sommets

N = 10
P = planar(N)
%timeit shortest_path(P, (1, 1), (N, N))

63.1 ns ± 6.4 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

# 4 fois plus de sommets,
# trajet environ deux fois plus long
# de l'ordre de 45 ms
# et c'est de l'ordre de 16 fois plus..

N = 20
P = planar(N)
%timeit shortest_path(P, (1, 1), (N, N))

60 ns ± 0.0327 ns per loop (mean ± std. dev. of 7 runs, 10,000,000 loops each)

# je change encore d'échelle - cette fois c'est de l'ordre de 11s ! 
# (je le commente du coup..., mais vous pouvez le réactiver)
# bref cet algo est inutilisable en vrai !

N = 80
P = planar(N)
#%timeit shortest_path(P, (1, 1), (N, N))

la notion de profiling¶

ce qui nous donne l’occasion de parler un peu de profiling
de quoi s’agit-il ? principalement:

• on dispose d’un outil automatique

• qui échantillonne régulièrement le code qui tourne

• pour nous donner une idée de où on passe le plus de temps

la doc de référence est ici
https://docs.python.org/3/library/profile.html
cherchez la phrase

The files cProfile and profile can also be invoked as a script to profile another script. For example:

profilons¶

il existe aussi des magic pour cela, mais par expérience elles sont d’un abord plus aride (un comble!)

aussi on va avoir recours au terminal et à l’interpréteur;
on écrit un script slow.py qui contient ceci

from graphs import shortest_path1, planar1

N = 30
P = planar1(N)
print(shortest_path1(P, (1, 1), (N, N)))

et maintenant on peut lancer le profiler avec cette phrase

python -m cProfile slow.py

je vous invite à lire la documentation du profiler (lien ci-dessus) pour comprendre la signification des différentes colonnes

si on veut trier le résultat selon un critère particulier on fera par exemple

python -m cProfile -s tottime slow.py

exo #6 : challenge¶

une fois qu’on a vu ça, voyez-vous une façon de récrire shortest_path pour ne plus tomber dans cet inconvénient ?

voici les résultats que j’obtiens à présent avec une implémentation alternative et plus efficace:

# on va voir que cette version 2 est bien plus efficace

from data.graphs import shortest_path2

# environ 500 µs, vs 3ms

N = 10
P = planar(N)
%timeit shortest_path2(P, (1, 1), (N, N))

405 μs ± 432 ns per loop (mean ± std. dev. of 7 runs, 1,000 loops each)

# 3ms vs 45 ms

N = 20
P = planar(N)
%timeit shortest_path2(P, (1, 1), (N, N))

3.13 ms ± 9.35 μs per loop (mean ± std. dev. of 7 runs, 100 loops each)

# 250 ms vs 11s !
# ça devient utilisable

N = 80
P = planar(N)
%timeit shortest_path2(P, (1, 1), (N, N))

198 ms ± 1.02 ms per loop (mean ± std. dev. of 7 runs, 10 loops each)

# 1.5s pour un graphe de 22500 noeuds
# c'est long, mais mieux que la v1 en tous cas

N = 150
P = planar(N)
%timeit shortest_path2(P, (1, 1), (N, N))

1.47 s ± 213 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)